Adi Satrio Ardiansyah, S.Pd., M.Pd., is a young lecturer in the Department of Mathematics at the Faculty of Mathematics and Natural Sciences, Universitas Negeri Semarang, with the main course of Mathematics Learning Innovation. Currently, he is also active in the field of student affairs as a Mentor for the Mathematics Student Association (HIMATIKA) at the Faculty of Mathematics and Natural Sciences, Universitas Negeri Semarang. His email address is adisatrio[a]mail.unnes.ac.id.
The main focus of mathematics education nowadays is the development of mathematical thinking and working patterns. This results in mathematics teachers needing to design learning that encourages students to have mathematical skills, such as creative thinking patterns because mathematics has an important meaning for thinking, seeing, and organizing the world [1], [2], [3], [4]. In contrast to its existence, mathematics is still a specter for students in Indonesia. The results of PISA 2018 and TIMSS 2015 show that Indonesia ranks 73 out of 79 countries and 44 out of 49 countries, respectively [5], [6]. These results are a wake-up call for mathematics educators, so that teachers as the front line in the process of implementing mathematics education need to pay attention to several challenges in the era of the industrial revolution and the 21st century.
As one of the qualifications that must be possessed by graduates in the era of the industrial revolution and the 21st century, creativity is of the essence and plays an important role in the process of solving mathematical problems [7], [8], [9], [10], [11]. Creative teachers can complete their tasks quickly and efficiently, including preparing online learning during the COVID-19 pandemic, as the use of platforms such as e-learning or learning management systems (LMS) needs to be prepared to accommodate distance learning [12], [13], [14]. Thus, students can explore themselves through self-learning because they can learn anywhere, anytime, and with any source available on the internet, and geographical differences and financial limitations can be accommodated through online learning without considering attendance in the classroom [15], [16].
To ensure the achievement of students’ creative thinking skills during online learning, a suitable learning model needs to be prepared that can accommodate students’ learning needs while still maintaining educational quality. The Challenge-based on Synchronous Online Course integrated with STEM-Context (CBSO-STEM) learning model is an innovative mathematics learning model that accommodates students’ needs during online classes. The Challenge Based Learning (CBL) framework provides a unique nuance to developing students’ skills through activities that guide students to solve the challenges given. The challenges given are framed as a problem that students must solve in group discussions. In addition, the role of the Synchronous Online Course strategy makes it easy for students to interact directly with their peers or with lecturers through various platforms and Learning Management Systems so that some material problems can be easily discussed. STEM itself, defined as a learning activity and nuance in the given problem, is the best integration for developing skills through meaningful and real-life learning processes using an Engineering approach and the use of technology, so that students can design solutions to the challenges given. The teaching and learning process is also aligned with science and mathematics, and relevant subjects, so that it can train students to collaborate and communicate problems in learning activities. The following is the syntax of the CBSO-STEM model and the STEM problem context presented in the Riemann Sum material.

STEM-Context on Riemann Sum Material
Big Idea

One of the parts of the Gadang House in Padang, West Sumatra that successfully fascinates many people is its roof. Made of ijuk and having a shape resembling buffalo horns, it symbolizes the Minangkabau tribe’s victory in buffalo racing competitions in Java. The curved and pointed shape of the roof is also often called gonjong. Before becoming a complete roof, the framework of the Padang house roof is in the form of parts that will be filled to become a complete roof. With the knowledge of integral calculus, we can calculate the area of the roof of the Gadang House in Padang, West Sumatra, by its parts. The parts of the roof to be assembled are actually based on the concept of Riemann sum partition.
Essential Question
Do you think we can find the area of the roof of the Padang house? If so, how do you find the roof area of a Padang house with the roof partitions?
STEM-Context on Integral Application Material
Big Idea

Have you ever noticed the shape of the steel wires hanging on a suspension bridge? Take a look at the picture of the Akashi-Kaikyo Bridge above the Akashi Strait, connecting Maiko in Kobe city to Awaji Island, Japan. If you observe closely, the curve formed by the wires resembles a parabolic curve. If we know the equation of the curve, we can easily calculate the length of wire required without actually stretching the wire. Moreover, we can also determine the area enclosed by the curve and the roadway. Calculus can be used to solve such cases.
Essential Question
How to determine the length of wire needed on the bridge? How do you determine the area of the region bounded by the curve? Is it possible to solve in several ways/different resolution methods?
STEM-Context on Material Transcendental Functions
Big Idea

Bactrocera carambolae, commonly known as the Star Fruit Fly, is one of the pests commonly found in several fruit plants such as mangoes, oranges, guavas, star fruits, etc. Its existence is very disruptive and difficult to control. In an experiment related to the growth of fruit flies, a number of fruit flies were placed in an environment that supports their growth, meaning they had enough food, temperature, and were inaccessible to predators. The experiment recorded the number of fruit flies present after t days in N(t) and then looked for the relationship between t and N(t). The results of the experiment are recorded in the following list.

Essential Question
Based on the data, what function can represent the data? How to obtain the function of the number of fruit fly populations based on this data? How about the geometric interpretation of the experimental results?
The implementation of the CBSO-STEM model in Integral Calculus courses was designed for sixteen meetings in the Even Semester of the Academic Year 2021/2022. The implementation was carried out in three experimental classes, namely the B class of the Mathematics Education Study Program, the Mathematics Study Program, and the Applied Statistics and Computation D3 Study Program. After filling out a perspective questionnaire regarding online learning and taking a pretest in the first meeting, students will learn Integral Calculus material for thirteen meetings by implementing the CBSO-STEM model. In the eighth and sixteenth meetings, students will take midterm and final exams as posttests. The following presents descriptive statistical results related to students’ mathematical creativity.
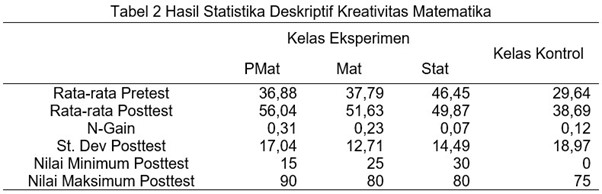
The results show that the average value of the experimental class for each implemented program using the CBSO-STEM model is not significantly different, ranging from 49 to 57. In addition, the experimental class average for each program implemented with the CBSO-STEM model is higher than the control class average, where the experimental class for the S1 Mathematics Education, S1 Mathematics, and D3 Applied Statistics and Computation programs each obtained an average value of 56.04, 51.63, and 49.87, respectively, while the control class only obtained 38.69. Furthermore, there was an increase in mathematical creativity in the experimental class for each program implemented with the CBSO-STEM model of 0.31, 0.23, and 0.07, respectively. It is evident that there is a difference between the pretest and posttest values in the experimental class for each program implemented with the CBSO-STEM model. The minimum value of the experimental class is 15 for S1 Mathematics Education, 25 for S1 Mathematics, and 30 for D3 Applied Statistics and Computation, while the minimum value of the control class is 0. The maximum value of the experimental class is 90 for S1 Mathematics Education, 80 for S1 Mathematics, and 80 for D3 Applied Statistics and Computation, while the maximum value of the control class is only 75. Further statistical tests need to be conducted to demonstrate the level of significance of these statements.
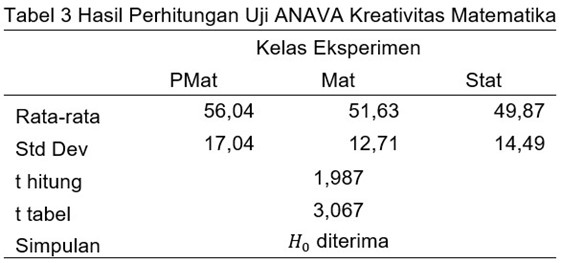
shown in Table 3 for mathematical creativity with the help of Excel, the calculated value of t is 1.987. With α = 5%, the tabulated value is obtained as ttab = 3.067. Since the calculated value of t = 1.987 < 3.067 = ttab, H0 is accepted. Thus, it can be concluded that there is no significant difference in the average mathematical creativity of students in the experimental classes of each program study that implements the CBSO-STEM learning model. In other words, the difference between classes that implement the CBSO-STEM model does not affect students’ mathematical creativity.
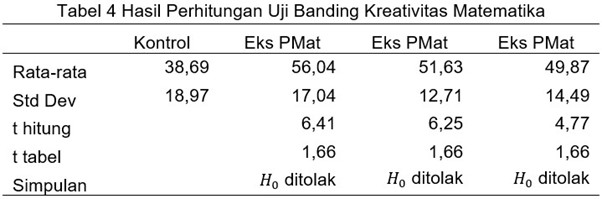
Based on the results of the mathematical creativity test as presented in Table 4, the average of the experimental class for S1 Mathematics Education and the average of the control class were 56.04 and 38.69, respectively. The results were then tested with a t-test, resulting in a t-value of 6.41 and a t-table value of 1.66. Since the t-value of 6.41 > t-table of 1.66, H0 is rejected. Therefore, the average mathematical creativity of the experimental class in S1 Mathematics Education is higher than the average mathematical creativity of the control class. Thus, it can be concluded that the CBSO-STEM model has a better impact on mathematical creativity for students in the S1 Mathematics Education program.
Based on the results of the mathematical creativity test presented in Table 4, the averages for the experimental class and control class mathematical creativity for the S1 Mathematics program were 51.63 and 38.69, respectively. The results were then tested with a t-test, resulting in a t-value of 6.25 and a t-table value of 1.66 with α = 5%. Since the t-value of 6.25 > t-table of 1.66, the null hypothesis (H0) is rejected. Therefore, it can be concluded that the average mathematical creativity of the experimental class in the S1 Mathematics program is higher than that of the control class. Thus, it can be said that the CBSO-STEM model has a better impact on the mathematical creativity of students in the S1 Mathematics program.
Based on the results of the mathematics creativity test as presented in Table 4, the average scores for the experimental class of the Applied Statistics and Computation D3 program and the control class were 49.87 and 38.69, respectively. The results were then tested using a t-test, resulting in a t-value of 4.77 and a t-table value of 1.66. Since the t-value of 4.77 is greater than the t-table value of 1.66, H0 is rejected. Therefore, the average mathematics creativity score for the experimental class of the Applied Statistics and Computation D3 program is higher than that of the control class. Thus, it can be concluded that the CBSO-STEM model has a better impact on the mathematical creativity of students in the Applied Statistics and Computation D3 program.
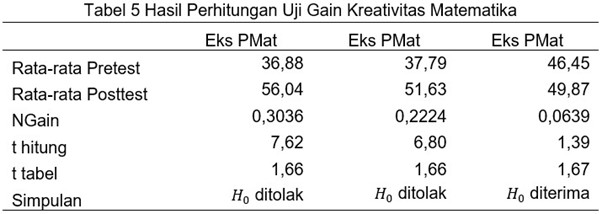
Based on the results of the mathematical creativity test presented in Table 5, the average pretest score for the experimental class of Mathematics Education S1 and the average posttest score for the experimental class of Mathematics Education S1 were 36.88 and 56.04, respectively. These results were then tested using a t-test, resulting in a calculated t-value of 7.62 and a critical t-value of 1.66. Since the calculated t-value of 7.62 is greater than the critical t-value of 1.66, the null hypothesis (H0) is rejected. Therefore, it can be concluded that the average posttest score for mathematical creativity in the experimental class of Mathematics Education S1 is higher than the average pretest score. In other words, there is a significant improvement in mathematical creativity in the experimental class of Mathematics Education S1 that has implemented the CBSO-STEM model. Furthermore, after calculating Ngain, a score of 0.3036 was obtained with a moderate criterion. Thus, it can be said that the CBSO-STEM model has a positive impact on improving the mathematical creativity of students in the Mathematics Education S1 program.
Based on the results of the mathematical creativity test presented in Table 5, the average pretest score for the experimental class of Mathematics S1 and the average posttest score for the experimental class of Mathematics S1 were 37.79 and 51.63, respectively. These results were then tested using a t-test, resulting in a calculated t-value of 6.80 and a critical t-value of 1.66. Since the calculated t-value of 6.80 is greater than the critical t-value of 1.66, the null hypothesis (H0) is rejected. Therefore, it can be concluded that the average posttest score for mathematical creativity in the experimental class of Mathematics S1 is higher than the average pretest score. In other words, there is a significant improvement in mathematical creativity in the experimental class of Mathematics S1 that has implemented the CBSO-STEM model. Furthermore, after calculating Ngain, a score of 0.2224 was obtained with a low criterion. Thus, it can be said that the CBSO-STEM model has a positive impact on improving the mathematical creativity of students in the Mathematics S1 program.
Based on the results of the mathematics creativity test as presented in Table 5, the average pretest score of the experimental class D3 Applied Statistics and Computation and the average posttest score of the experimental class D3 Applied Statistics and Computation were 46.45 and 49.87, respectively. These results were then tested using a t-test, resulting in a t-value of 1.39 and a t-table value of 1.67. Since the t-value of 1.39 ≤ 1.67 = t-table, H0 is accepted. Therefore, the average posttest mathematics creativity score of the experimental class D3 Applied Statistics and Computation is equal to the average pretest mathematics creativity score of the same class. In other words, there is an insignificant improvement in mathematics creativity in the experimental class D3 Applied Statistics and Computation that has implemented the CBSO-STEM model. Furthermore, after calculating Ngain, a value of 0.0639 was obtained, indicating a low impact. Thus, it can be concluded that the CBSO-STEM model has an impact on improving the mathematics creativity of students in the D3 Applied Statistics and Computation program with a low level of success.
After attending Integral Calculus lectures implementing the CBSO-STEM model, students were asked to fill out a questionnaire regarding their response to the implementation of the CBSO-STEM learning model. There were 40 statements classified into several aspects related to the implementation of the CBSO-STEM model in Integral Calculus lectures. These aspects are: (1) the implementation aspect of synchronous activities; (2) the implementation aspect of the LMS; (3) the implementation aspect of Virtual Meetings; (4) the implementation aspect of discussion activities; (5) the implementation aspect of the availability of teaching materials; (6) the implementation aspect of the availability of instructional videos; (7) the implementation aspect of student-centered activities; (8) the implementation aspect of assignments; and (9) students’ opinions on the implementation of the CBSO-STEM model. The following are the results of the students’ response to the implementation of the CBSO-STEM model in Integral Calculus lectures.

The score for the aspect of synchronous activity implementation is 3.36 with a Good category, the score for the aspect of LMS implementation is 3.36 with a Good category, the score for the aspect of virtual meeting implementation is 3.31 with a Good category, the score for the aspect of discussion activity implementation is 3.49 with a Very Good category, the score for the aspect of availability of learning resources is 3.41 with a Very Good category, the score for the aspect of availability of instructional videos is 3.37 with a Good category, the score for the aspect of student center activity implementation is 3.22 with a Good category, the score for the aspect of assignment implementation is 3.45 with a Very Good category, and the score for the aspect related to students’ opinion on the implementation of the CBSO-STEM model is 3.25 with a Good category. These results indicate a positive response from students towards the implementation of the CBSO-STEM model, with a final score of 3.36 (good category).
The innovation of the CBSO-STEM learning model provides an alternative solution for online learning that takes into account students’ needs while ensuring the quality of learning outcomes. The CBSO-STEM model has the potential to develop creative thinking skills and other skills needed by students.
Challenge Based Learning provides students with opportunities to develop the 4C skills [17]. Group discussions provide students with the experience of working in teams effectively. In its implementation, students work on challenges in groups where each member is involved in finding ideas to solve the given challenge, thus developing students’ collaborative skills [18], [19].
At the beginning of the learning process, students will be presented with a Big Idea. The Big Idea presented should have a meaningful connection between the content material and students’ lives, in order to motivate them to learn. Then, students are asked to provide Essential Questions related to the presented Big Idea. This learning experience provides an opportunity for students to ask questions, thus developing their critical thinking skills. Next, students will be asked to complete a given challenge. The challenge needs to be developed from a situation and activity that can create a sense of urgency and prompt student action. This learning experience can encourage students to develop critical thinking skills.
In solving the challenges, students are given several guides such as activity guides, question guides, and material guides that provide opportunities for students to make decisions with the hope of developing their responsibility. Students are given a safe space to think creatively, try new ideas, experiment, fail, receive feedback, and try again. In the journey of solving the challenges, every solution presented by students is valued, and there needs to be an evaluation for each process. This learning experience can develop students’ creativity. Findings reveal that the implementation of the Challenge Based Learning model can improve students’ mathematical creative problem-solving skills, creative thinking skills, and mathematical creativity. Furthermore, almost 88% of students agreed that they became more creative individuals after participating in the Challenge Based Learning experience because Challenge Based Learning can be developed in a very flexible and creative situation and provides a safe space for all students to think creatively, try new ideas, experiment, fail, receive feedback, and try again.
The results of the challenge solutions are well-documented by students and will be useful for continuous reflection, informative assessment, evidence of learning, portfolio, and telling their Challenge stories. After students successfully find the solutions to the challenges, they are asked to publish their findings. The students findings will be evaluated by students and teachers to obtain the best challenge solution results. This publishing activity provides students with the opportunity to express their opinions, ideas, criticisms, and suggestions in written and oral forms, thus developing students communication skills.
STEM education is based on real-life problems that lead students to seek solutions to social, economic, and environmental issues [30]. When integrating STEM into math education, there are several things to consider: (1) using meaningful learning that is related to students’ daily lives; (2) challenging students’ potential by using an engineering approach to develop critical and creative thinking skills through related activities; (3) providing students with technology designs and learning from failures in designing engineering solutions with existing designs; (4) implementing a teaching and learning process that aligns with science, math, and relevant subjects such as language, humanities, and social studies; and (5) training students to collaborate and communicate problem-solving in learning activities [31].
Synchronous class activities are a suitable option because students can interact directly with each other to discuss a learning topic and both the teacher and students can interact with each other at the same time even though they are in different places. Online communication helps students stay connected with their classes and classmates through a platform like a WhatsApp Group. This is called synchronous learning because the system allows students to ask questions to their teacher or classmates instantly through instant messaging and provides students with immediate feedback from their teacher [13]. Furthermore, teachers will provide feedback through virtual meeting activities.
The learning model was then analyzed for its effectiveness by considering several criteria. The research results showed that (a) the CBSO-STEM model showed similar average mathematical creativity scores for experimental class students from each implemented study program using the CBSO-STEM learning model, (b) the average mathematical creativity of students with the CBSO-STEM model was better than the average mathematical creativity of students with the expository model, (c) the CBSO-STEM model showed an improvement in the mathematical creativity of students who implemented the CBSO-STEM learning model, and (d) students gave a positive response to the implementation of the CBSO-STEM learning model. In other words, it can be concluded that the implementation of the CBSO-STEM model is effective in developing students’ mathematical problem-solving abilities.
The implementation of the CBSO-STEM model is one alternative solution in the implementation of online learning. The application of this model can be further developed to develop other skills/abilities of students considering the need for graduate qualifications in the era of Industry 4.0 and IT developments.
References:
[1] R. Zevenbergen, S. Dole, and R. J. Wright, Teaching Mathematics in Primary Schools. New South Wales: National Library of Australia, 2004.
[2] Suherman, Strategi Pembelajaran Matematika Kontemporer. Bandung: JICA, 2003.
[3] H. Hudojo, Pengembangan Kurikulum dan Pembelajaran Matematika. Surabaya: UM Press, 2003.
[4] I. Junaedi and M. Asikin, “Pengembangan Pembelajaran Matematika Humanistik Untuk Meningkatkan Kemahiran Matematis,” Unnes J. Math. Educ. Res., vol. 1, no. 2, 2012.
[5] A. Schleicher, PISA 2018: Insights and Interpretations. OECD Publishing, 2019.
[6] I. V. S. Mullis, M. O. Martin, P. Foy, and M. Hooper, Timss 2015 International Results in Science Saved. IEA, 2015.
[7] A. Malik, “Creating Competitive Advantage through Source Basic Capital Strategic Humanity in the Industrial Age 4 . 0,” Int. Res. J. Adv. Eng. Sci., vol. 4, no. 1, pp. 209–215, 2019.
[8] L. Prifti, M. Knigge, H. Kienegger, and H. Krcmar, “A Competency Model for ‘Industrie 4.0’ Employees,” Proc. der 13. Interantionalen Tagung Wirtschaftsinformatik, pp. 46–60, 2017, [Online]. Available: https://www.wi2017.ch/images/wi2017-0262.pdf.
[9] A. Benešová and J. Tupa, “Requirements for Education and Qualification of People in Industry 4.0,” Procedia Manuf., vol. 11, no. June, pp. 2195–2202, 2017, doi: 10.1016/j.promfg.2017.07.366.
[10] E. Levenson, “Tasks that may occasion mathematical creativity: Teachers’ choices,” J. Math. Teach. Educ., vol. 16, no. 4, pp. 269–291, 2013, doi: 10.1007/s10857-012-9229-9.
[11] A. Fatah, D. Suryadi, J. Sabandar, and Turmudi, “Open-ended approach: An effort in cultivating students’ mathematical creative thinking ability and self-esteem in mathematics,” J. Math. Educ., vol. 7, no. 1, pp. 9–18, 2016, doi: 10.22342/jme.7.1.2813.9-18.
[12] G. Hema and S. M. Gupta, “Adversity Quotient (AQ) for Prospective Higher Education,” Int. J. Indian Psychol., vol. 2, no. 3, 2015.
[13] C. W. Huang, J. Y. Liao, C. S. Wang, and Z. Y. Su, “An Analysis of the Performance of Synchronous Online English Tutoring,” Int. J. Online Pedagog. Course Des., vol. 10, no. 2, pp. 21–36, 2020, doi: 10.4018/ijopcd.2020040102.
[14] J. M. Zydney, Z. Warner, and L. Angelone, “Learning through experience: Using design based research to redesign protocols for blended synchronous learning environments,” Comput. Educ., vol. 143, no. August 2019, p. 103678, 2020, doi: 10.1016/j.compedu.2019.103678.
[15] R. C. Choe et al., “Student satisfaction and learning outcomes in asynchronous online lecture videos,” CBE Life Sci. Educ., vol. 18, no. 4, pp. 1–14, 2019, doi: 10.1187/cbe.18-08-0171.
[16] J. E. Nieuwoudt, “Investigating synchronous and asynchronous class attendance as predictors of academic success in online education,” Australas. J. Educ. Technol., vol. 36, no. 3, pp. 15–25, 2020, doi: 10.14742/AJET.5137.
[17] A. S. Ardiansyah, G. Hanafi, and N. Dwi, “Upaya Mengembangkan Keterampilan 4C melalui Challenge Based Learning,” vol. 5, pp. 627–637, 2022.
[18] R. S. Cheung, J. P. Cohen, H. Z. Lo, and F. Elia, “Challenge Based Learning in Cybersecurity Education,” vol. 1, 2011.
[19] J. Malmqvist, K. Kohn Rådberg, and U. Lundqvist, “Comparative analysis of challenge-based learning experiences,” Proc. 11th Int. CDIO Conf., 2015.
[20] Nurlaili, D. Afriansyah, and Y. A. Nuri, “Pengaruh Model Pembelajaran Challenge Based Learning Tehadap Kemampuan Berpikir Kritis Siswa Pada Materi Lingkungan Kelas X Di SMA NEGERI 4 Prabumulih,” J. Pena Sains, vol. 4, no. 2, pp. 97–104, 2017, [Online]. Available: http://journal.trunojoyo.ac.id/penasains/article/download/3209/Berpikir kritis.
[21] S. Nawawi, “Developing of module challenge based learning in environmental material to empower the critical thinking ability,” J. Inov. Pendidik. IPA, vol. 3, no. 2, p. 212, 2017, doi: 10.21831/jipi.v3i2.15988.
[22] S. Junita, “Peningkatan Kemampuan Creative Problem Solving Matematis Siswa Smp Dengan Pendekatan Challenge Based Learning,” J. Pengajaran MIPA, vol. 21, no. 1, pp. 19–23, 2016, doi: http://dx.doi.org/10.18269/jpmipa.v21i1.656 PENINGKATAN.
[23] A. S. Ardiansyah, I. Junaedi, and M. Asikin, “Student’s Creative Thinking Skill and Belief in Mathematics in Setting Challenge Based Learning Viewed by Adversity Quotient,” Unnes J. Math. Educ. Res., vol. 7, no. 1, pp. 61–70, 2018.
[24] A. S. Ardiansyah, R. Fariz, and K. Khoirunnisa, “Prespektif Gender terhadap Kemampuan Berpikir Kreatif Mahasiswa pada Blended Learning berbantu Google Classrooms,” vol. 11, no. 2, pp. 245–255, 2020.
[25] A. S. Ardiansyah and M. Asikin, “Challenging students to improve their mathematical creativity in solving multiple solution task on challenge based learning class,” J. Phys. Conf. Ser., vol. 1567, no. 2, pp. 4–10, 2020, doi: 10.1088/1742-6596/1567/2/022088.
[26] A. S. Ardiansyah and I. Junaedi, “Tingkat kreativitas matematika siswa dalam menyelesaikan muliple solution task setting challenge based learning ditinjau dari kemampuan matematika dan perbedaan gender,” Pros. Semin. Nas. Mat. 3, vol. 3, pp. 258–265, 2020.
[27] L. Johnson and S. Adams, Challenge Based Learning: The Report from Implementation Project. Austin, Texas: The New Media Consortium, 2011.
[28] M. Nichols, K. Cator, and M. Torres, “Challenge Based Learning Guide,” Digit. Promise Chall. Inst., p. 59, 2016.
[29] D. Palenti and R. Zulkarnain, “Challenge-Based Learning and Collaborative Skills,” J. Nonform. Educ., vol. 5, no. 2, pp. 167–173, 2019, [Online]. Available: https://journal.unnes.ac.id/nju/index.php/jne/article/view/20221.
[30] D. Acar, N. Tertemiz, and A. Tasmedir, “The Effects of STEM Training on the Academic Achievement of 4th Graders in Science and Mathematics and their Views on STEM Training,” Int. Electron. J. Elem. Educ., vol. 10, no. 4, pp. 505–513, 2018. [31] S. Bahrum, N. Wahid, and N. Ibrahim, “Integration of STEM education in Malaysian and why to STEAM,” Int. J. Acad. Res. Bus. Soc. Sci., vol. 7, no. 6, pp. 645–654, 2017.





